CS/Network
[Network] Routing algorithms - Link State
최블랙
2021. 12. 13. 18:30
라우팅 알고리즘의 목적
라우팅 알고리즘의 목적은 출발지 라우터에서 목적지 라우터까지 최단 비용으로 갈 수 있는 길을 찾는 것이다.
라우팅 알고리즘 종류
라우팅 알고리즘에는 두가지 종류가 있다.
- Link State algorithm: 모든 라우터들의 정보를 가지고 있을 경우
- Distance Vector algorithm: 자신과 이웃한 라우터의 정보만 가지고 있을 경우
Link State algorithm
기본 가정
각 라우터는 이웃한 라우터의 정보만을 가지고 있다.
그럼 어떻게 모든 라우터의 정보를 얻을 수 있을까 ❔

각 라우터는 모든 라우터에게 이웃한 라우터의 정보를 브로드캐스트해 네트워크의 전체 그림을 얻는다. 이후 각 라우터는 독립적으로 자신으로부터 모든 라우터까지 최단 거리를 계산한다.
어떻게 라우터는 다른 라우터까지 최단 거리를 계산할까 ❔❔
라우터는 다익스트라(Dijkstra) 알고리즘을 사용해 최단 거리를 계산한다!
Pseudo code
c(i, j): 노드 i에서 j의 링크 비용
D(v): 출발지에서 v까지 오는데 걸리는 현재 비용
p(v): 이전 노드
N': 출발지에서 어떤 노드까지 오는데 걸리는 비용이 최소인 노드들의 부분집합
Initialization:
N ’= {u};
for all nodes v
if v adjacent to u
then D(v) = c(u, v);
else D(v) = MAX_VALUE;
Loop
find w not in N’ such that D(w) is a minimum;
add w to N’;
update D(v) for all v adjacent to w and not in N’:
if D(w) + c(w, v) < D(v) then
// w gives us a shorter path to v than we’ve found so far
D(v) = D(w) + c(w, v);
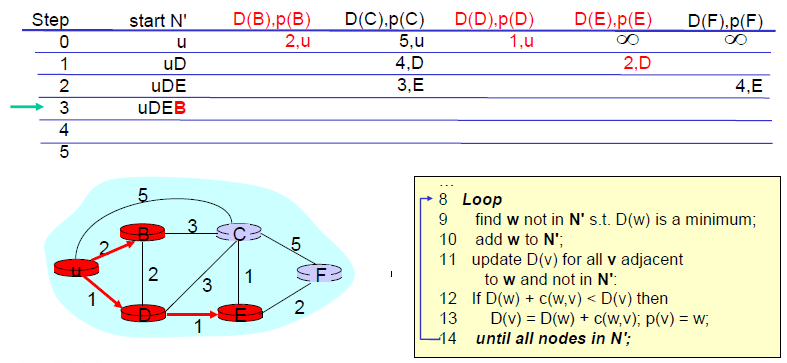
until N’ = N;예시
1. u에서 시작한다고 가정하면 u와 인접한 B, C, D는 cost를 저장하고 나머지 노드는 현재 정보를 알 수 없기 때문에 최대값을 저장한다.
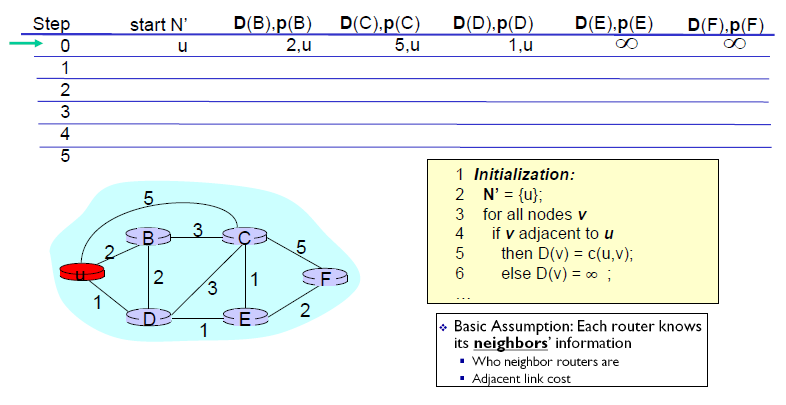
2. N'에 포함되지 않는 노드 중 최소 비용을 가지는 노드(u)를 선택한다.

3. 최소 비용을 가지는 노드(u)를 N'에 포함시킨다.
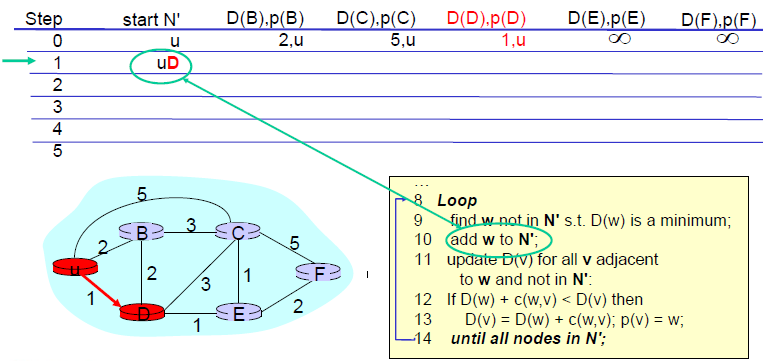
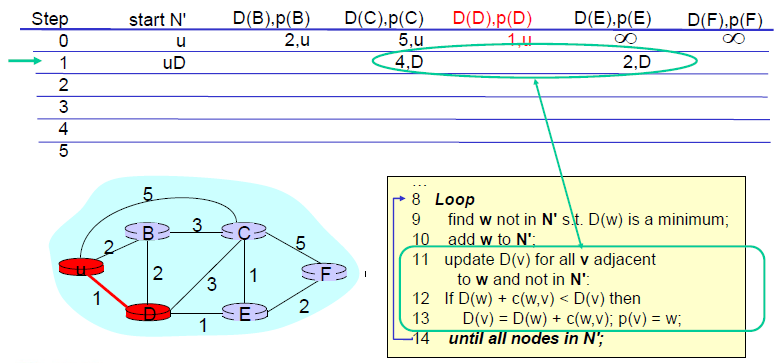
4. 선택한 노드와 인접하고 N'에 포함되지 않은 모든 노드의 비용을 수정한다.
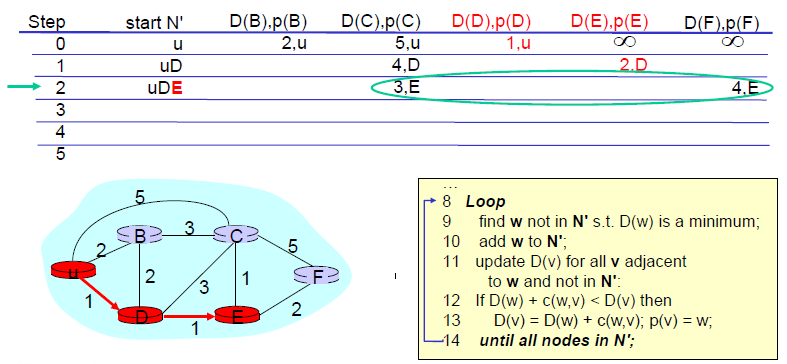
5. 모든 노드가 N'에 포함될 때까지 이를 반복한다.

시간 복잡도
다익스트라 알고리즘의 시간 복잡도는 N 노드가 있을 때 반복해서 N'에 포함되지 않은 모든 노드를 확인하고 값을 수정하기 때문에 O(n^2)의 시간 복잡도를 가진다.
하지만 heap 자료구조를 사용할 경우 O(nlogn)으로 더 효율적인 구현이 가능하다.