[Network] Routing algorithms - Distance Vector
이 포스팅은 앞선 Routing Protocols - link state 다음으로 이어진다.
라우팅 알고리즘의 목적
라우팅 알고리즘의 목적은 출발지 라우터에서 목적지 라우터까지 최단 비용으로 갈 수 있는 길을 찾는 것이다.
라우팅 알고리즘 종류
라우팅 알고리즘에는 두가지 종류가 있다.
- Link State algorithm: 모든 라우터들의 정보를 가지고 있을 경우
- Distance Vector algorithm: 자신과 이웃한 라우터의 정보만 가지고 있을 경우
Distance Vector algorithm
기본 가정
각 라우터는 이웃한 라우터의 정보만을 가지고 있다.
어떻게 다른 라우터까지의 최소 비용 경로를 찾을 수 있을까 ❔❔
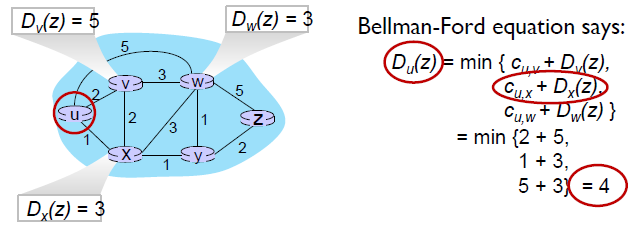
각 라우터는 Distance Vector를 가지고 있다. 이 distance vector는 모든 라우터에 대한 추정된 최소 비용 경로를 말한다. 각 라우터는 이웃한 라우터와 DV를 교환한다. DV를 받은 라우터는 Bellman-Ford equation을 사용하여 추정된 비용이 감소했으면 distance vector를 수정한다. 이를 계속 반복하면 추정된 최소 비용 경로는 실제 최소 비용 경로에 수렴하게 된다.
Bellman-Ford equation
정의

x에서 y로 가는 최소 비용 경로(dx(y))는 x와 이웃한 모든 정점 v에서 y로 가는 최소 비용 + x에서 v로 가는 최소 비용의 최솟값이다.
예시
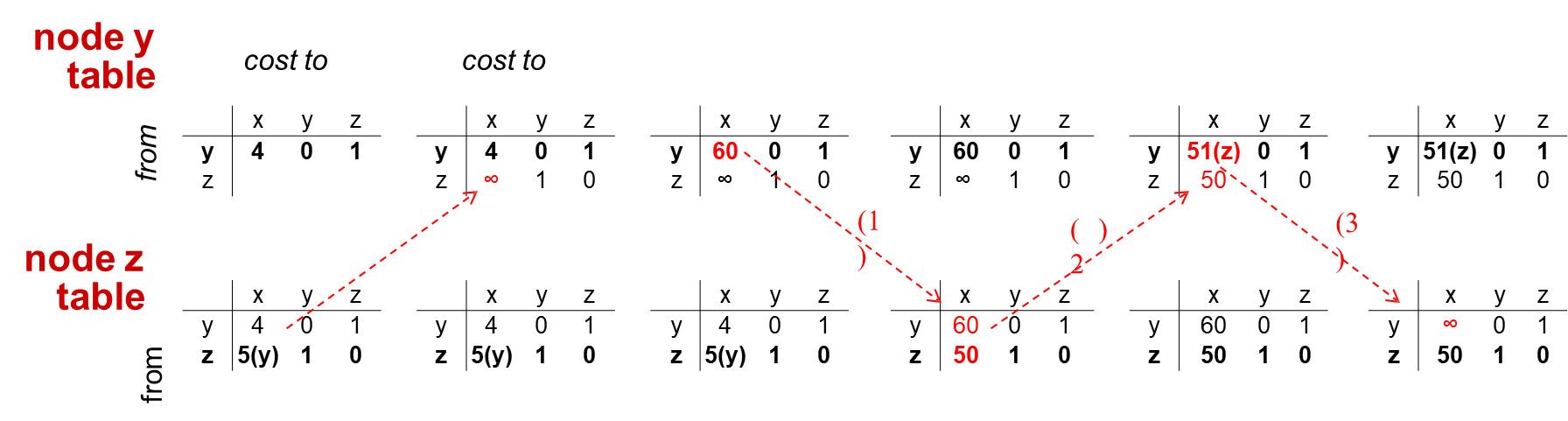
Distance Vector 예시
초기 다음과 같은 x, y, z 라우터가 DV를 가지고 있다고 가정해보자. 각 라우터는 이웃한 라우터와 DV를 교환한다.

이웃한 라우터의 DV를 받고 Bellman-Ford equation을 사용하여 추정된 비용이 감소했으면 distance vector를 수정한다.

DV의 변화가 없을 때까지 계속 반복한다.

만약 링크 비용이 바뀌면 어떻게 될까 ❔❔
라우터가 링크 비용이 바뀐 것을 감지하면, 라우팅 정보를 수정하고 DV를 다시 계산한다. 이후 DV가 바뀌었다면, 이웃한 라우터에게 DV를 전달한다.
다음과 같이 x에서 y로 가는 비용이 4에서 1로 바뀌었다고 가정해보자.

라우터 y는 DV를 다시 계산하고 DV를 x와 z에게 전달한다. y의 DV를 받은 z는 DV를 수정하고 이웃한 x, y에게 전달한다. 이후 어떤 라우터의 DV도 변화가 없기 때문에 일을 종료한다.

만약 다음과 같이 x에서 y로 가는 비용이 4에서 60로 바뀌었다고 가정해보자.

y는 x로 가는 경로가 60이고, z가 x로 가는 최소 경로 dz(x)가 5라는 것을 알기 때문에 더 비용이 작은 z를 통해 가는 경로를 택할 것이고, dy(x)는 c(y, z) + dz(x)가 되어 6이 될 것이다. 이와 같은 방식으로 DV의 변화가 있다면 수정하고 이웃한 라우터에게 DV를 전달할 것이다. 이는 y에서 x로 가는 최소 비용 경로가 51이 될 때까지 반복할 것이다.


만약 수가 더 커진다면 계속해서 참조가 발생하게 될 수 있다. 이를 Count-to-infinity problem이라고 한다. 하지만 초기에 y는 z를 거쳐 x로 가는 경로를 택하면 안 된다.
why? z에서 x로 가는 최소 경로 dz(x)가 y를 거쳐 가는 길이기 때문이다. 실제 이 경로는 y → z→ y → x가 되지만 z는 y→ x 경로의 비용이 수정됐다는 것을 모르기 때문에 이러한 문제가 발생하는 것이다.
Count-to-infinity 문제를 어떻게 해결할 수 있을까 ❔❔
Count-to-infinity 문제가 발생한 결정적인 이유는 왔던 경로를 되돌아가기 때문이다. (y → z→ y → x) 이를 방지하기 위해 최소 경로를 계산할 때 결정적인 역할을 했던 이웃 라우터에게 경로 비용을 무한대라고 전달한다. 이를 Poisioned reverse라고 한다.
만약 위의 예시와 같이 z 라우터가 y를 거쳐 x로 가는 것이 최소 비용 경로라면, z는 y에게 z에서 x로 가는 경로는 무한대의 비용이 발생한다라고 전달한다.
예시